วันนี้ขอเสนอบทความที่เกี่ยวกับช่างเทคนิคหรือวิศวกรซักเล็กน้อยครับ สืบเนื่องจากมีโอกาสได้ไปเกี่ยวดองหนองยุ่งกับกะทะล้อและล้อแม็กรถยนต์ มีคำถามจากเพื่อนๆว่าจะวัดขนาดของ pitch circle diameter บนกะทะล้อหรือล้อแมกซ์ซึ่งเป็นตำแหน่งที่เราต้องเจาะรูเพื่อยึดกะทะล้อหรือล้อแม็กได้อย่างไร เป็นคำถามที่ช่างทุกคนตอบได้ไม่ยาก หากจำนวนรูเจาะเป็น 4 รู, 6 ,8 รู ซึ่งจะมีรูเจาะที่อยุ่ตรงข้ามกันและเมื่อลากเส้นจากจุดศูนย์กลางของรูเจาะทั้งสองจะพบว่าเส้นดังกล่าวผ่านจุดศูนย์กลางของกะทะหรือล้อแม็กพอดี โดยระยะห่างระหว่างศูนย์กลางของโบลต์ 2 ตัวที่อยู่ตรงกันข้ามกัน จะเป็นขนาดของ pitch circle diameter แต่หากเป็น 5 รู ดังแสดงในภาพที่ 1 วิธีการวัดบนกะทะล้อหรือล้อแม็กดังกล่าวจะไม่สามารถกระทำได้ ดังนั้นในบทความนี้จึงขอนำเสนอวิธีการหา pitch circle diameter ของกะทะล้อหรือล้อแม็กที่จำนวนรูเจาะ n ใดๆ โดยไม่จำกัด
ภาพที่ 1 กะทะล้อแบบ 5 รูเจาะ
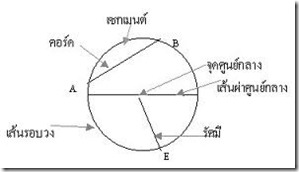
ก่อนอื่นขอให้ท่านผู้อ่านทบทวนพื้นฐานและสมบัติของรูปวงกลม ดังแสดงในภาพที่ 2 ครับ
ภาพที่ 2 สมบัติของวงกลม
ในบทความนี้ขอให้ท่านผู้อ่านพิจารณา คอร์ด AB ครับ ซึ่งจะเป็นพื้นฐานของการหา pitch circle diameter สมบัติของคอร์ด กล่าวไว้ว่า
- ถ้าส่วนของเส้นตรงผ่านจุดศูนย์กลางของวงกลม และตั้งฉากกับคอร์ดที่ไม่ใช้เส้นผ่านศูนย์กลาง แล้วส่วนของเส้นตรงนั้นจะแบ่งครึ่งคอร์ด
- ถ้าส่วนของเส้นตรงผ่านจุดศูนย์กลางของวงกลม และแบ่งครึ่งคอร์ดที่ใช่เส้นผ่านศูนย์กลางแล้ว ส่วนของเส้นตรงนั้นจะตั้งฉากกับคอร์ด
จากสมบัติทั้งสองข้อของคอร์ด แสดงได้ดังภาพที่ 3
หากท่านผู้อ่านจินตนาการว่าจุด A และ จุด B คือจุดศูนย์กลางของรูเจาะสองรูที่อยู่ใกล้กันบนกะทะล้อหรือล้อแม็ก เมื่อเราลากเส้นตรงจากจุดศูนย์กลาง O ของกะทะล้อหรือล้อแม็กไปยังจุด A และ B เราจะได้สามเหลี่ยม หน้าจั่ว OAB เนื่องจากเส้นตรง OA และ OB มีความยาวเท่ากันเท่ากับรัศมีของ pitch circle diameter หากพิจารณาสามเหลี่ยมย่อย AOC และ BOC เราจะพบว่า
มุม AOC = มุม BOC เนื่องจากสมบัติของสามเหลี่ยมหน้าจั่ว
ดังนั้น มุม AOC = มุม AOB /2
มุม AOB คือมุมรองรับเซกเมนต์ AB
ภาพที่ 4 รูปร่างเรขาคณิตของกะทะล้อหรือล้อแม็ก
การประยุกต์หา pitch circle diameter ของกะทะล้อและล้อแม็ก
ให้ท่านผู้อ่านจินตนาการว่าหากมีรูเจาะทั้งหมด n รู รอบ pitch circle diameter (PCD) เราจะพบคอร์ดทั้งหมด n คอร์ด
มุมรองรับของแต่ละคอร์ด = 360/n
จากรูปสามเหลี่ยม AOC จากความสัมพันธ์ทางตรีโกณมิติเราจะได้ว่า
AC = OA*sin(AOC) (1)
หาก AC = AB/2 , OA = PCD/2 , มุม AOC = 360/(2*n)
แทนค่าลงในสมการ 1 จะได้
AB/2 = (PCD/2)sin(180/n)
จัดรูปใหม่เป็น
PCD = AB/sin(180/n) (2)
หรือ PCD = m*AB
เมื่อ m = 1/sin(180/n)
เมื่อ PCD = pitch circle diameter
AB คือ ความยาวคอร์ด AB หรือระยะห่างระหว่างจุดศูนย์กลางของรูเจาะที่อยู่ติดกัน
n คือจำนวนรูเจาะ
ท่านผู้อ่านคงจะเห็นว่า การหา pitch circle diameter ของกะทะหรือล้อแม็ก จะสามารถคำนวณได้จากความยาวของระยะห่างระหว่างจุดศูนย์กลางของรูเจาะที่อยู่ติดกัน
ในทางปฏิบัติ ช่างหรือวิศวกรที่อยู่หน้างานก็ต้องวัดระยะห่างระหว่างจุดศูนย์กลางของรูเจาะที่อยู่ติดกันทั้งหมด n ค่าและนำมาหาค่าเฉลี่ย (สูตร excel ใช้ average ) เพื่อให้มีความถูกต้องมากขึ้น ในขณะเดียวกันการวัดระยะห่างระหว่างจุดศูนย์กลางของรูเจาะที่อยู่ติดกันควรจะกระทำขณะที่กะทะล้อหรือล้อแม็กสวมอยู่จะเป็นการสะดวกและได้ค่าที่ถูกต้องกว่า ท่านผู้อ่านอาจจะเขียนสูตรใน excel เพื่อช่วยให้คำนวณได้ง่ายขึ้น โดยเราจะพบว่าค่า m เป็นค่าคงที่และสามารถนำมาใช้สูตร excel ดังนี้
= 1/sin(radiand(180/B3)) หากกำหนดให้จำนวนรูเจาะถูกบันทึกไว้ที่ cell B3 ค่า m ที่จำนวนรูเจาะต่างๆกันแสดงเป็นตัวอย่างได้ในตารางที่ 1
= 1/sin(radiand(180/B3)) หากกำหนดให้จำนวนรูเจาะถูกบันทึกไว้ที่ cell B3 ค่า m ที่จำนวนรูเจาะต่างๆกันแสดงเป็นตัวอย่างได้ในตารางที่ 1
ตารางที่ 1 ตัวคูณคำนวณสำหรับคำนวณ PCD ของกะทะล้อหรือล้อแม็ก
| จำนวนรูเจาะ | m |
| 4 | 1.4142 |
| 5 | 1.7013 |
| 6 | 2.0000 |
| 8 | 2.6131 |
| 10 | 3.2361 |
สรุปขั้นตอนการหาตำแหน่งรูเจาะบนกะทะล้อหรือล้อแม็กนะครับ
- นับจำนวนรูเจาะ
- วัดระยะห่างระหว่างจุดศูนย์กลางของรูเจาะที่อยู่ติดกันจำนวนเท่ากับรูเจาะ
- หาค่าเฉลี่ยของระยะห่างระหว่างจุดศูนย์กลางของรูเจาะที่อยู่ติดกัน
- คำนวณค่า pitch circle diameter ของกะทะหรือล้อแม็ก ตามสมการที่ 2 หรือใช้ค่า m ตามตารางที่ 1
หวังว่าจะเป็นประโยชน์ให้กับท่านผู้อ่านนะครับ สวัสดีครับ






1 ความคิดเห็น:
ขอบคุณครับ
แสดงความคิดเห็น