หากให้ x เป็นรากที่ n ของจำนวนจริง C ใดๆ เราสามารถเขียนเป็นสมการได้ดังนี้
หากทำการยกกำลัง n ทั้งสองข้างของสมการและจัดรูปแบบสมการใหม่สามารถเขียนได้เป็น

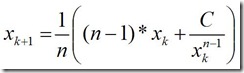
x(k) คือค่าประมาณการครั้งที่ k
จากสมการนี้ เราสามารถใช้ VBA เพื่อทำการคำนวณแบบทำซ้ำเพื่อหารากที่ n ของจำนวนจริง C ใดๆได้ โดยเริ่มต้นการคำนวณครั้งแรกต้องเดาค่า x เริ่มต้นก่อน และการคำนวณจะสิ้นสุดลงเมื่อ x(k+1) มีการเปลี่ยนแปลงค่าอยู่ในช่วงที่ยอมรับได้เมื่อเทียบกับค่า x(k) วิธีการคำนวณเช่นนี้จะเรียกว่า ระเบียบวิธีการของ นิวตันราฟสัน (Newton Rapson Method) ซึ่งเคยนำเสนอในบทความต้นๆของ blog นี้มาแล้วโดยใช้ฟังก์ชัน Goal Seek
โค้ดใน VBA สามารถแสดงได้ดังภาพ
VBA Code (For…Next)
จาก VBA Code นอกจากจะแสดงวิธีการคำนวณเชิงตัวเลขเพื่อหาค่ารากที่ n ของจำนวนจริงใดๆแล้ว ยังเป็นการแสดงวิธีการใช้คำสั่ง For…Next และการออกจากลูปเมื่อเงื่อนไขที่กำหนดไว้เป้นจริง (เงื่อนไขการตรวจสอบความละเอียดของผลการคำนวณ) โดยในความเป็นจริงแล้ว การคำนวณลักษณะนี้น่าจะใช้คำสั่ง While….Wend จะเหมาะสมกว่า ลองปรับเปลี่ยนโค้ดและนำไปใช้งานดูนะครับ
อ้อท่านผู้อ่านจะเห็นว่า subrutene นี้ยังใช้งานได้ไม่สะดวกเนื่องจากไม่สามารถรับค่าเข้ามาคำนวณได้ หากเปลี่ยนเป็นฟังก์ชันโดยกำหนดให้รับค่าจำนวนจริง C ใดๆและอันดับของราก n ด้วยแล้วจะทำให้มีความยืดหยุ่นในการใช้งานมากยิ่งขึ้นครับ ดังแสดงในภาพ
VBA Code (While…Wend)
จากภาพเราจะเรียกใช้ฟังก์ชัน Root ผ่าน macro ชื่อ test โดยผ่านค่า C และ n จาก เซลล์ B1 , B2 และคืนค่ารากที่ n กลับมาแสดงในเซลล์ B3 ครับ โดยรากที่ n ของ C ที่คำนวณได้จะมีความละเอียดถึง 15 ตำแหน่ง และใน code ที่ผมนำเสนอได้มีการป้องกัน Excel value ที่ไม่พึงประสงค์ไว้ด้วยลองทำความเข้าใจในโค้ดดูนะครับ





ไม่มีความคิดเห็น:
แสดงความคิดเห็น